Day 0 – Intervals and the major scale
Hello and welcome to the 5-day basic music theory songwriting challenge!
Before we begin Day 1 (tomorrow), we must first agree on a few basic basics like intervals.
As always, you’ll find a (slightly shorter) video version of today’s proceedings at the bottom of this page.
Let’s go!
1. Intervals (part I)
Intervals are the distances between notes. They are important because they determine how they behave with each other. Obviously, you don’t behave the same way when your parents are around. Or do you?
Anyway, the unit of measurement and shortest distance between two notes (at least in Western music) is the semitone (half step).
That’s the interval between the notes on any two adjacent frets on the guitar or any two adjacent keys on the piano.
The piano is trickier because the interval between two adjacent white keys is a semitone only if there is no black key between them, e.g. between E and F or between B and C.
If there IS a black key between two white keys, they are not adjacent (just… trust me on this one) and the interval between them is a tone (whole tone, whole step), e.g. between C and D or between F and G.
On the guitar that interval equals 2 frets.
I’m tempted to say that the interval between any two black keys is also a tone, as it is between C# and D# or G# and A#, but of course there are larger gaps there between D# and F# and between A# and C# which add up to not 2, but 3 semitones (3 frets on the guitar).
And it goes on like this.
2. The major scale
The piano is good for one thing.
If you look at the white keys, it gives you an instant snapshot of the major scale (the only scale we’ll use this week).
To build the major scale we only need two intervals – the tone and the semitone:
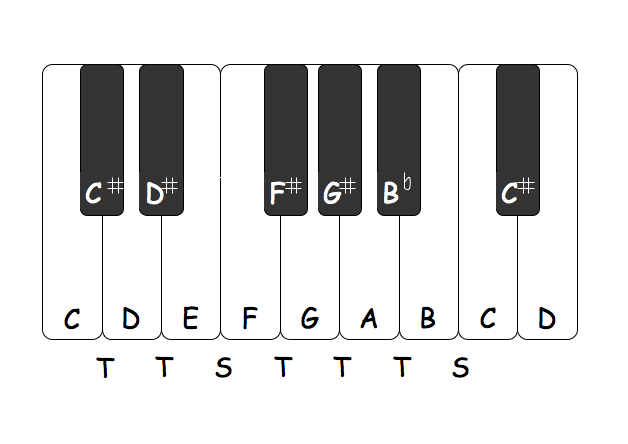
C D E F G A B is the C major scale, because it stars on C.
C is the 1st degree of the scale, D – the 2nd degree, E – the 3rd, etc.
There is a tone between degrees 1 and 2, 2 and 3, 4 and 5, 5 and 6 and 6 and 7, and there is a semitone between degrees 3 and 4 and 7 and 8 (8 bearing the same name as 1).
Back to the snapshot — the black keys show where the whole tones are and the missing black keys are where the semitones are.
You can also think about the major scale as a sequence of tones and semitones:
T T S T T T S
or whole and half steps:
W W H W W W H
You can build the major scale on any note and this sequence of intervals will be the same.
On the piano different major scales yield different snapshots of the keyboard, but on the guitar, if you use only one string, you see that the interval pattern is the same:
with the 1st degree on the open string (fret 0) you will have to fret frets 2, 4, 5, 7, 9 and 11 for degrees 2, 3, 4, 5, 6 and 7 of the scale respectively:
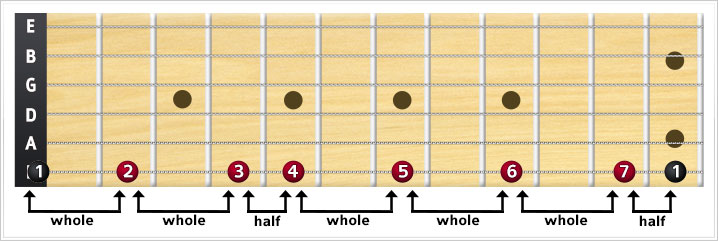
On the G-string for example that will give you the notes G A B C D E and F# — the G major scale. Notice how F was raised to F# to conform to the pattern requiring a whole tone between degree 6 and 7 and a semitone between degree 7 and 8.
3. Intervals (part II)
The positions of notes in the major scale are useful for remembering the names of intervals.
The interval between the 1st and the 2nd degree is a second.
The interval between the 1st and the 3rd degree is a third, between the 1st and the 4th — a fourth, between the 1st and the 5th — a fifth, etc.
Only the interval between the 1st degree and itself is called a unison and the one between the 1st and the 8th degree (bearing the same name because that’s where the scale loop ends) is an octave.
Some intervals have a major and a minor version — the second, the third, the sixth and the seventh — the minor version being a semitone smaller than the major one.
Others are perfect — the fourth and the fifth — they remain unchanged in major and minor scales.
To compare intervals we measure them in tones or semitones.
So here are the basic intervals to know:
Minor second = semitone = 1 semitone (e.g. between E and F)
Major second = whole tone = 2 semitones (e.g. between C and D)
Minor third = 3 semitones (e.g. between A and C or between D and F)
Major third = 4 semitones (e.g. between C and E or between G and B)
Perfect fourth = 5 semitones (e.g. between C and F or between D and G)
Perfect fifth = 7 semitones (e.g. between C and G or between E and B)
An octave = 12 semitones (e.g between C and the next C or between D and the next D)
Intervals are important because they determine how notes relate to each other (friends, enemies, colleagues, parents and kids).
In melodies, intervals describe shapes.
In chords, intervals determine quality and colour.
And in context all of those carry an emotional charge.
We’ll see more about this in Day 1 and 2.
4. Origins
We have now effectively worked our way back to the origins of Western music. Here’s Leonard Bernstein elegant retelling of how the intervals we just saw actually appeared in reverse order — from the octave down to the semitone following the gradual assimilation of the intervals from the harmonic series.
5. Homework
As homework, you can try building the major scale on D, A, E, F, Bb and Eb (and if you’re feeling adventurous, on B and C# as well).
You can also try building intervals — start with octaves, fifths and major and minor thirds — from as many different notes as you have time for.
If you play the guitar, try playing intervals on more than one string, with the ultimate goal of playing the major scale on more than one string.
That’s all for Day 0.
Any questions? Ask away in the comments below.
Tomorrow we start with chords!
And here’s today’s video: