There’s beauty in simplicity. All it takes to move forward is one step. That’s how programmers teach computers to do stuff. One step at a time. Ones and zeroes. Algorithms.
But what do you do if one plus one does not yield an unequivocal result? When 1+1 = 1 (drop(s) of water), 1+1 = 2 (trees) and 1+1 = 3 (man+woman = man, woman and child)?
That’s the kind of dilemma we face in music. It’s deeply rooted in mathematics and yet numbers can’t (fully) account for its profound emotional ramifications (and robots can’t (quite) be taught how to write a (good) song).
Plus, digits in music seem confusing at first. What makes a half step more important than a whole one? Why are there 12 notes in the octave and not 8? How come a third can be both two steps and one step and a half?
Well, let’s try to make sense of this nonsense. If you can count to two, you can count to four, and that’s about all it takes to understand the math between the (staff) lines.
Before we get to twos though, let’s look at…
1. Zeroes and (fractions of) ones
Zero is unison. Staying on the same note. Not going anywhere. Plucking the same old string.
Now pluck half the string (fret at the 12th fret on the guitar). 1/2 of the string vibrates. You’re playing an octave higher.
Now fret a third of the string (7th fret). 2/3 of the string vibrate. You’re playing a perfect fifth above the original note.
Fret a fourth of the string (5th fret). 3/4 of the string vibrate. You’re playing a perfect fourth above the original note.
4/5 of the string? A major third above.
Etc.
You might have heard talk about frequency – how fast a string vibrates. Half a string vibrates twice as fast as the whole string, so its frequency is twice as high. The ratio of the frequencies of a note and the note an octave below it is 2:1 (as is the ratio of the lengths of string which vibrate).
The ratio of the frequencies of a note and the note a fifth below it is 3:2.
And so on. The same numbers as above, but upside down, because we’re going down instead of up and we’re lengthening instead of shortening the string.
But wait. I said we’ll count to two and then started dividing the one. Mea culpa. I just love fractions.
OK, let’s try this again.
2. Equals and halves
The above method of finding notes and defining intervals is called just intonation. It has to do with consonance and the physical nature of (see point 4. below).
The problem with tuning an instrument in just intonation is that it’s hard to use it to play in more than one key.
That’s why, towards the end of the 16th century, a tuning system was developed which divides the octave in 12 equal parts – 12-tone equal temperament or just equal temperament. (Bach, the new-tech nerd that he was, quickly wrote a album of songs for it in all 12 major and 12 minor keys.)
The advantage of equal temperament is not only that it allows playing a single instrument like the (well-tempered) piano or the (fretted) guitar in all keys (and with all singers), but also that it’s more or less close to just intonation, especially the perfect fifths and fourths, and so virtually indistinguishable from it, especially for people with less-than-acute ears, i.e. most people.
Yet another advantage is that, despite the fact it’s based on logarithms, equal temperament allows you and me to stop worrying about fractions and ratios and get by on basic arithmetic.
So, zero is unison.
One is a semitone – our basic unit of measurement, because the octave is divided into 12 of them. One is also called a half step by analogy to the awkward translation of “tone” as “step”.
So, adding one to one in a continuing effort at simplicity, we get to two, three and four.
If we want to jump more than one step at a time, we must tell the computer how many of these little steps it has to count before it makes the jump.
3 for a minor third.
4 for a major third.
5 for a fourth.
7 for a fifth.
12 for an octave.
3. Dozens, threesomes and fourdoms
But why 12? Why not 7 as in diatonic scales? Or 5 as in pentatonic scales?
Well, call it a product of magic and method, passion and reason, emotio and ratio. (What?! Not ratio again?!)
You know how in fairy tales (and rhetorical arguments) things come in threes? Brothers, daughters, bears, little pigs, guesses, magi… The Holy Trinity…
And how, to make sense of the madness (and time and space), we get on all fours? Points of the compass, quadrants, seasons, elements… Horsemen…
The greatest secret of the Three Musketeers? They were four.
Where did Four and Three meet? In myth class.
Do you see where this is going?
Multiply 3 x 4 and you get 12 months, 12 hours on the clock, 12 eggs in a dozen and… 12 notes in the octave!
Now add up 3 and 4 and you get the number of semitones (7) you need to find the note a fifth up from your starting note (the only other note you need to play a power chord and also the root on which to build the dominant for your tonic).
Divide 3 by 4 (three fourths of the string vibrate – see above) and you go up a fourth.
Divide 4 by 3 (four thirds vibrate) and you go down a fourth (to the fifth of your starting note (since 4/3 of a string is twice as long as 2/3 and thus an octave below it).
Count 4 semitones up from a note and you get the major third of your chord, count 3 more up and you get all the notes for a major triad.
Count 3 semitones up first and then 4 more and you get a minor triad.
Count 3 plus 3 up and you get a diminished triad.
(6 semitones also split the octave in half and give you the (dreaded in the Middle Ages) devil’s interval – the tritone – single-handedly responsible for the greatest amount of tension (and therefore resolution) this side of equal temperament.)
((+3+3+3 gives you the diminished seventh chord, which, by virtue of its symmetry and the 2 (two!) tritones it contains, can be inserted before ANY chord.))
Count 4 plus 4 semitones up for the augmented triad – another perfectly symmetrical chord which is great in passing.
Finally, subtract 3 from 4 to get back to square 1.
There! We’re past 0.
4. High fives and perfect fifths
But let’s give 5 and 7 their due too.
5, as we know, comes after 3 and 4, but is also, in musical terms, the inversion of 7. A perfect fourth (5 semitones) is the inversion of the perfect fifth (7 semitones) and vice versa, they complete each other to an octave. 5+7 = 7+5 = 12.
Now, let’s imagine counting up from our (same old) note in fives. +5+5+5+5… How long do you think before we reach a note of the same name?
5 and 12 don’t have a common denominator, which means you have to count up 12 times before you get to a note of the same name.
It’s the same for 7. In fact, because of inversion, going up in sevens is the same as going down in fives (and going down in sevens is the same as going up in fives). Again, it will be 12 times before we get to a note of the same name.
Sound familiar? This is the good old circle of fifths (or circle of fourths, if you go in the other direction). If you take Leonard Bernstein’s word for it (which you should), the accumulation of the fifth, the fifth of the fifth and the fifth of the fifth of the fifth is exactly how we got to 12 notes in the octave (the chromatic scale).
He talks about the gradual assimilation of the intervals of the harmonic series into harmony, which is actually a convenient intersection of counting half steps and calculating fractions.
The idea of harmonics is that when a string (column of air, etc.) vibrates, the halves, thirds, fourths of it, etc. vibrate as well producing a series of overtones of the fundamental (the whole string).
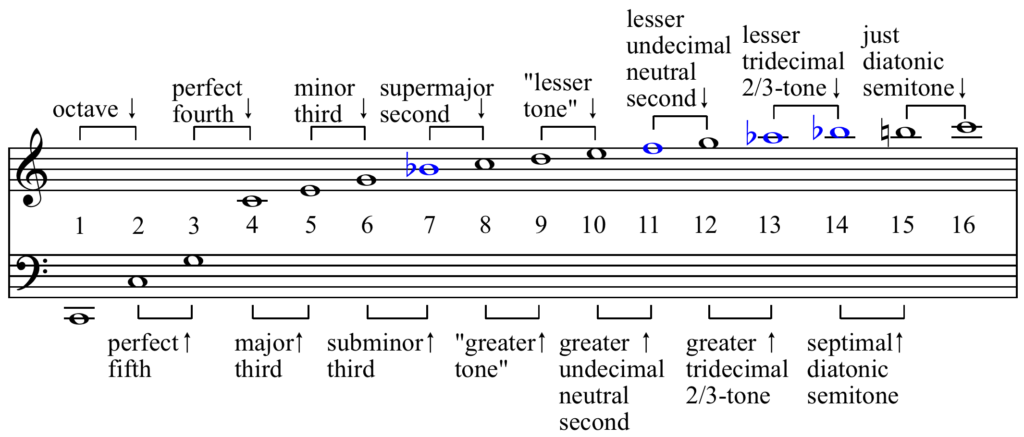
(picture by Hyacinth, CC BY-SA 3.0)
In point 1. above, we mentioned that the ratio of the frequencies (number of vibrations over time) of notes 3 and 2 in the above picture (a fifth apart) is 3/2. If you play them together, the higher note will vibrate 3 times for every 2 vibrations of the lower note, before they start vibrating together again. For notes 5 and 4 (a major third apart), the higher note will vibrate 5 times for every 4 vibrations of the lower note.
You can also think about it in terms of length of string. If you take the length of string of the lower note as the point of reference, you would need 2 lengths to fit in a whole number (3) of the length of the fifth above, which is 2/3 in length (2 = 6/3 = 3 x 2/3). Similarly, you would need 4 lengths of string to fit in an exact number (5) of major thirds, which are 4/5 of the string (4 = 20/5 = 5 x 4/5).
An excellent way to visualize consonance (why the first few intervals defined by the harmonic series sound good together) is to picture notes as sine waves.
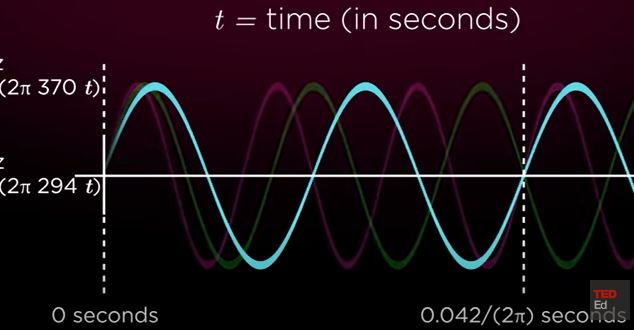
The waves of the notes in a major triad have compatible cycles (they meet at the 0-axis relatively often). That’s because their frequency ratios use relatively small numbers.
By contrast, a minor second (a semitone, our step 1, the building block of the 12-tone scale) is defined by a ratio of roughly 16 to 15 (the higher note’s frequency is 16/15 of the lower note’s; the higher note’s length of string is 15/16 of the lower note’s). It would take much longer for the waves of these two notes to align (you would need 16 lengths of string to fit a whole number of 15/16s in – much more than for the fifth or the major third).
That is why this interval is so dissonant and that is why it was so difficult to make this step even though it was (supposed to be) our first.
5. The stuff of math and myth
When I went to college after a childhood spent with British textbooks, I once wrote “maths” in an essay and my American instructor said she’d never heard the word before. She was the teacher so I assumed I had made a mistake, not knowing at the time that both words were correct (and referred to the same thing) but in different places.
Numbers are more absolute than words and yet, as I have tried to show you here, when it comes to music (as well as many other human activities), we find ways to temper their justness, bend them to our practical purposes, fiddle with them to suit our fuzzy logic.
Mathematics is a great tool to describe music and give us structured ways of understanding it, but we like a little bit of mess, don’t we? Some may even say that we can’t help it, because the world is inherently chaotic rather than ordered.
Hopefully, the above exploration of the numbers behind the sounds is structured enough to help you get a better grasp of the 12 notes you use every day, but also unstructured enough to let you keep some faith in the margin of error (and its meaningfulness).
Formulas, after all, will only get us so far. Once we exhaust them, we’ll have no choice but to go back and keep looking for the magic behind the mic.